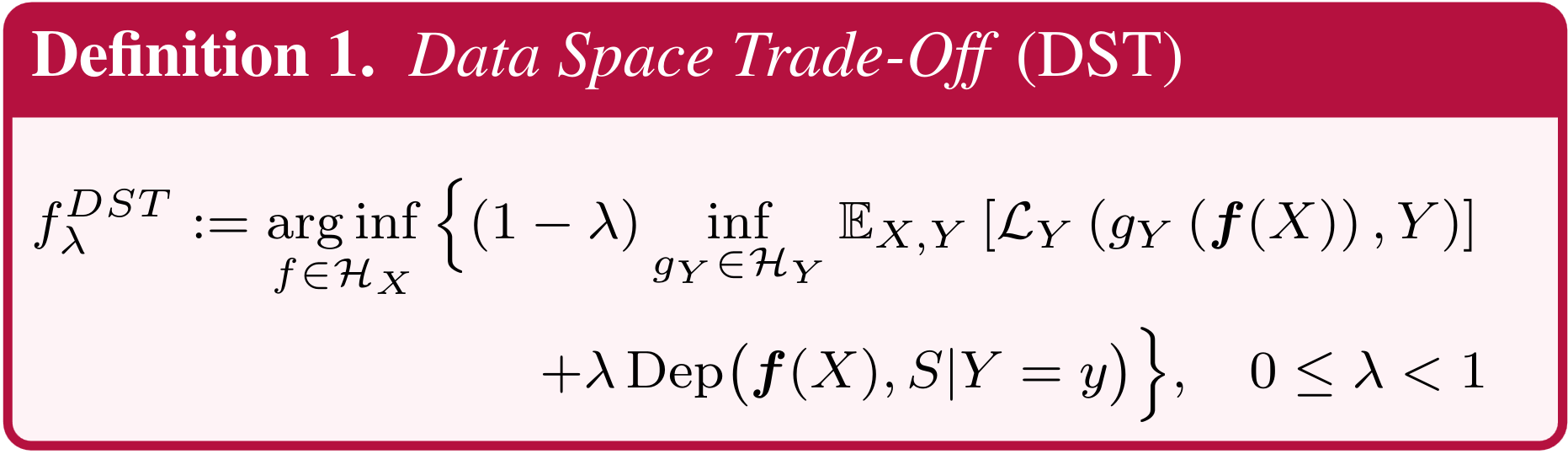Utility-Fairness Trade-Offs and How to Find Them

Sepehr Dehdashtian, Bashir Sadeghi, Vishnu N. Boddeti

{sepehr, sadeghib, vishnu} @ msu.edu

Michigan State University

How Fair is Your ML Model?

Let's assume that you have a model or you want to pick a pre-trained model for your task. The question that we should consider is that how fair is this model and how far is it from the best achievable utility-fairness point?

To answer these questions, we need to find the best achievable trade-off between utility and fairness. We call this trade-off DST which stands for Data Space Trade-Off. (next) This DST line finds the Possible region of this utility-fairness space where we expect all the models that are trained on this dataset to lie. By calculating the distance between the model and the DST line, we can measure how fair the model is and how much do we need to fine-tune our model.

Also, we are curious to know what is the intrinsic trade-off between the utility and fairness for a given pair of target attribute Y and sensitive attribute S. To address that, we need to find the best achievable trade-off regardless of the imperfection of the data samples. Basically in this case, we assume that we have the perfect samples that completely representing their corresponding labels. We call this trade-off LST which stands for Label Space Trade-Off. (next)

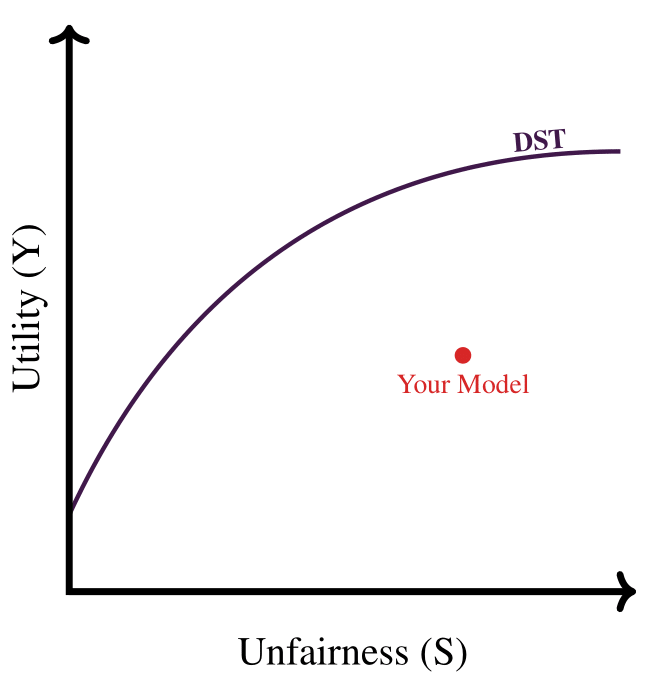
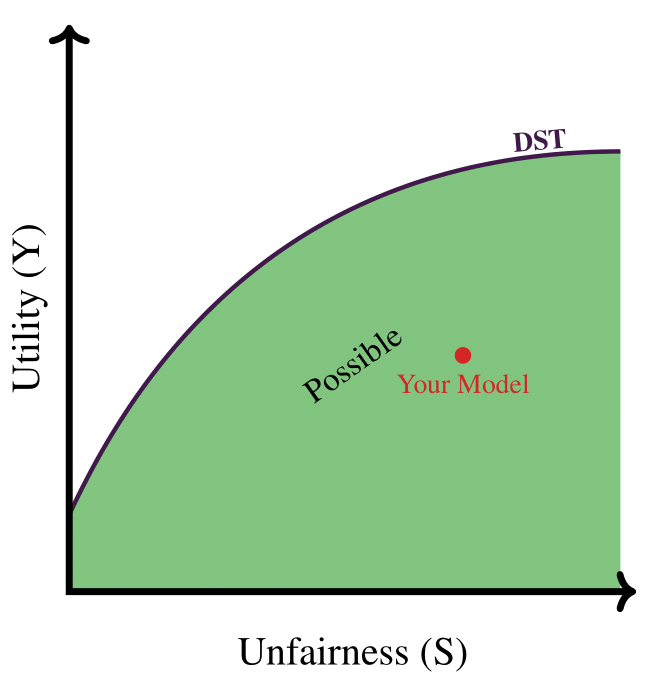
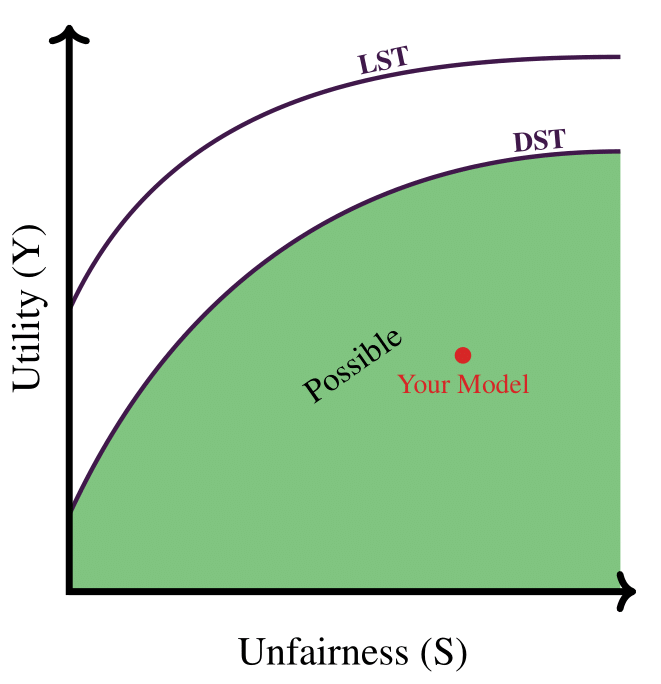
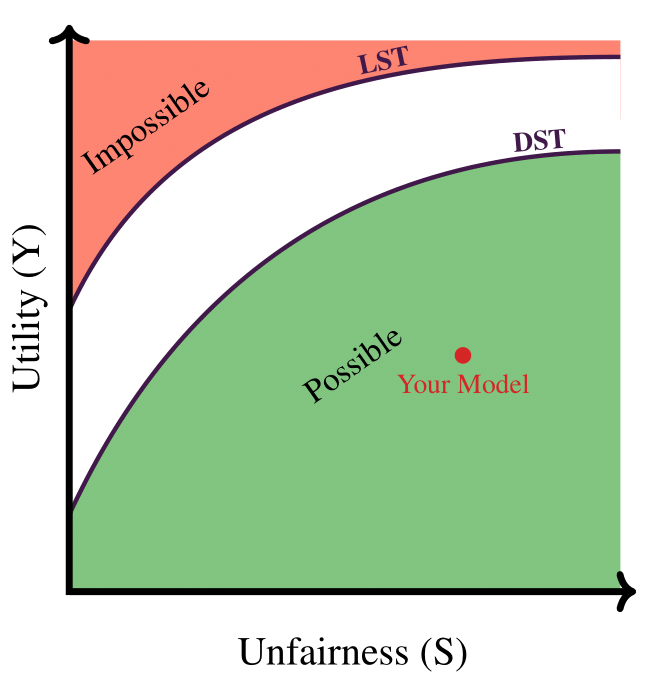
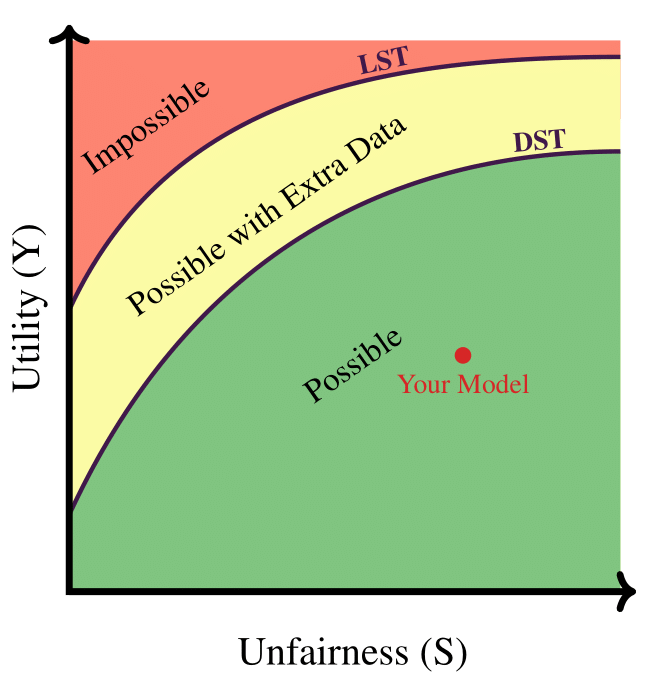
Questions that We Answer

What are the definitions of DST and LST?
How can we empirically estimate them?

Definitions

Fairness Definitions

Demographic Parity (DP) \[ P(\hat{Y} = 1 | {\color{red} S = s}) = P(\hat{Y} = 1 | {\color{red} S = s'}) \]
Equalized Opportunity (EO) \[ P(\hat{Y} = 1 | {\color{green} Y = 1}, {\color{red} S = s}) = P(\hat{Y} = 1 | {\color{green} Y = 1}, {\color{red} S = s'}) \]
Equality of Odds (EOO) \[ P(\hat{Y} = 1 | {\color{green} Y = 1}, {\color{red} S = s}) = P(\hat{Y} = 1 | {\color{green} Y = 1}, {\color{red} S = s'}) \\ \text{\&} \\ P(\hat{Y} = 1 | {\color{green} Y = 0}, {\color{red} S = s}) = P(\hat{Y} = 1 | {\color{green} Y = 0}, {\color{red} S = s'}) \]

We want to find these trade-offs for 3 different definitions of fairness:

1) Demographic Parity (DP): This definition requires that the probability of success should be the same for all the sensitive groups. This definition does not consider merit of the individuals.

2) Equalized Opportunity (EO): This definition requires that the probability of success should be the same among all the sensitive groups for the ones that deserve it.

3) Equality of Odds (EOO): This definition requires that the probability of true positive and also false positive be the same for all the sensitive groups.

How to Estimate these Trade-Offs?

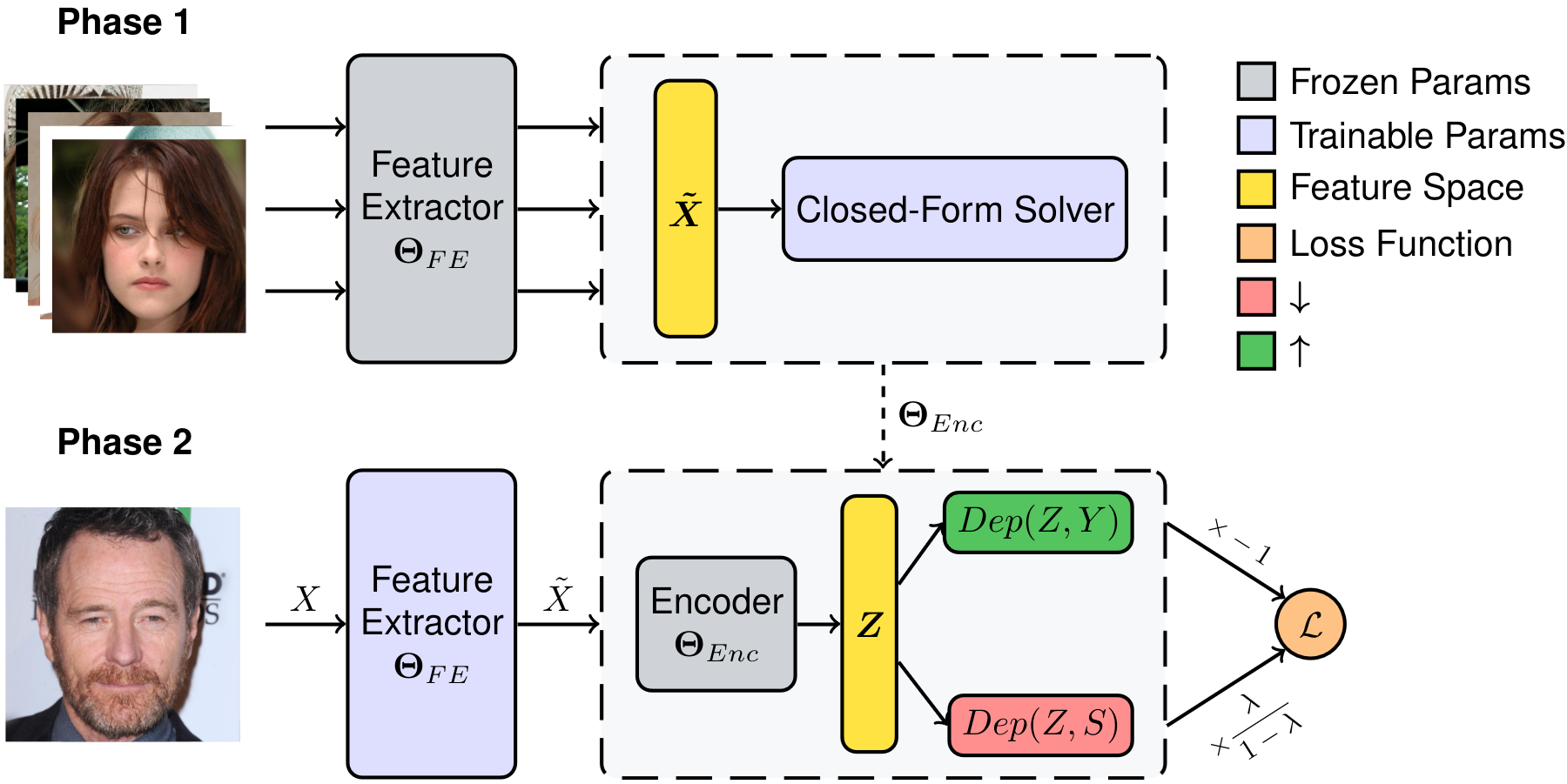
U-FaTE ( Utility-Fairness Trade-Off Estimator)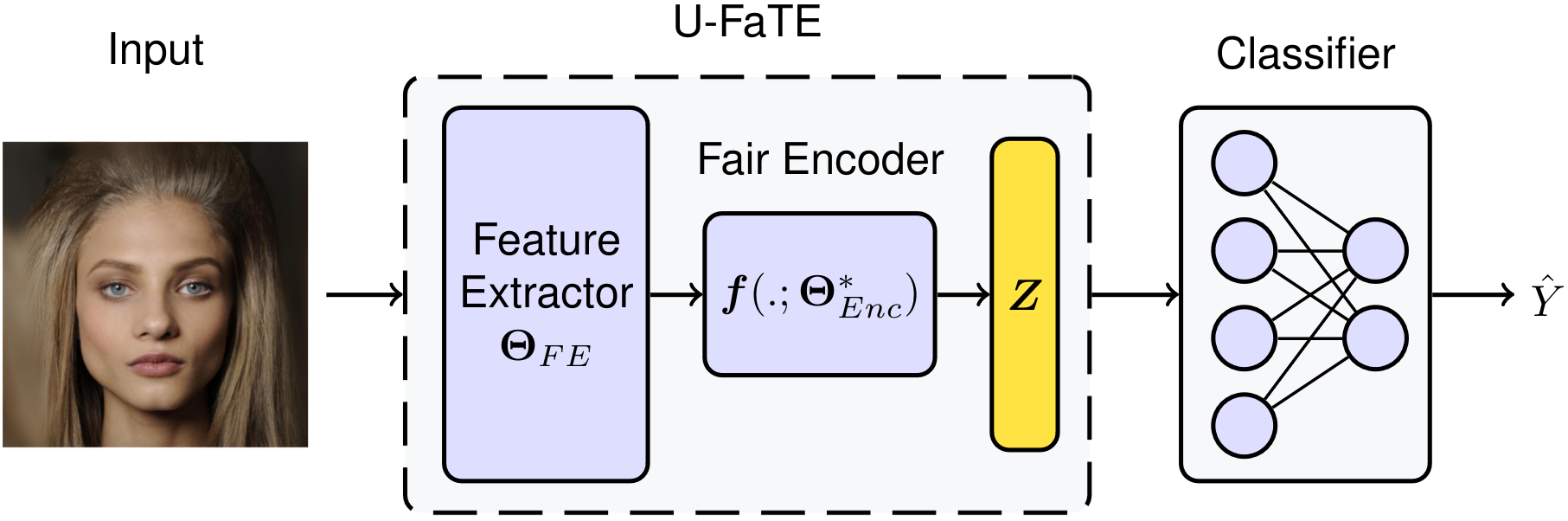 U-FaTE

Objective Function

\[ \min_{\Theta_{FE}, \Theta_{Enc}} \Big\{ \mathcal{L} = {\color{black}-\ \text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), Y)} {\color{black}\ +}\ \frac{\lambda}{(1 - \lambda)} {\color{black}\text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), S)}\Big\} \] \[ \min_{\Theta_{FE}, \Theta_{Enc}} \Big\{ \mathcal{L} = {\color{green}-\ \text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), Y)} {\color{black}\ +}\ \frac{\lambda}{(1 - \lambda)} {\color{black}\text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), S)}\Big\} \] \[ \min_{\Theta_{FE}, \Theta_{Enc}} \Big\{ \mathcal{L} = {\color{green}-\ \text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), Y)} {\color{red}\ +}\ \frac{\lambda}{(1 - \lambda)} {\color{red}\text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), S)}\Big\} \] \[ \min_{\Theta_{FE}, \Theta_{Enc}} \Big\{ \mathcal{L} = {\color{green}-\ \text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), Y)} {\color{red}\ +}\ {\color{purple} \frac{\lambda}{(1 - \lambda)}} {\color{red}\text{Dep}(f(X; \Theta_{FE}, \Theta_{Enc}), S)}\Big\} \]

Preserves
Y
Information

Trade-Off Control Parameter

Removes
S
Information

Training

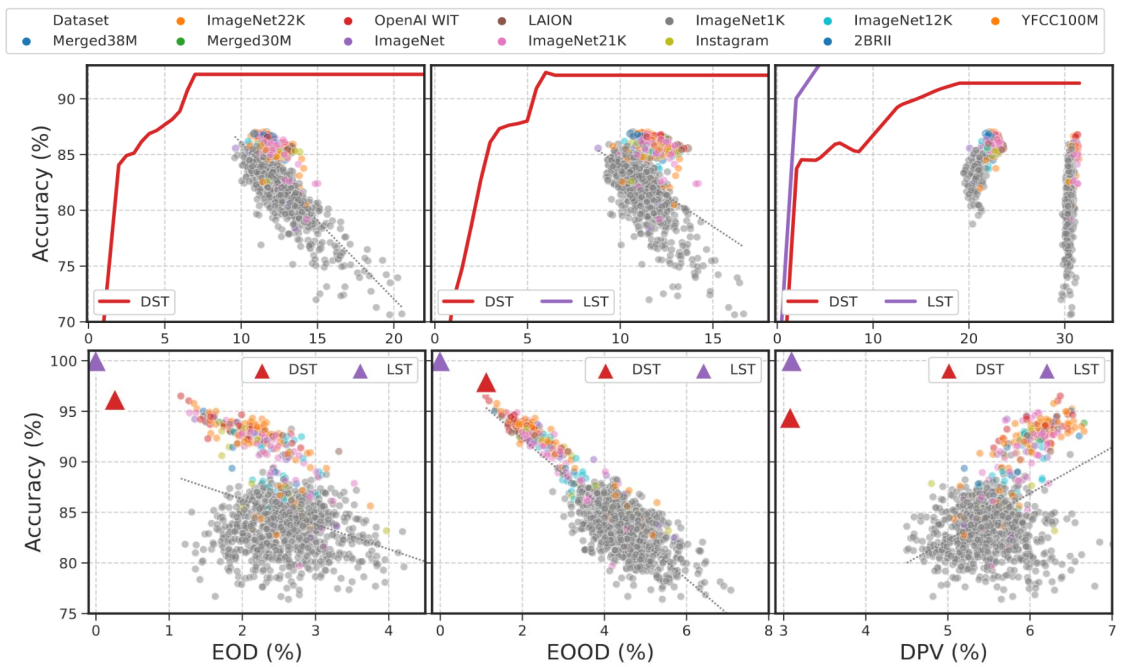
Experimental Evaluation

How far are existing FRL methods from the two trade-offs?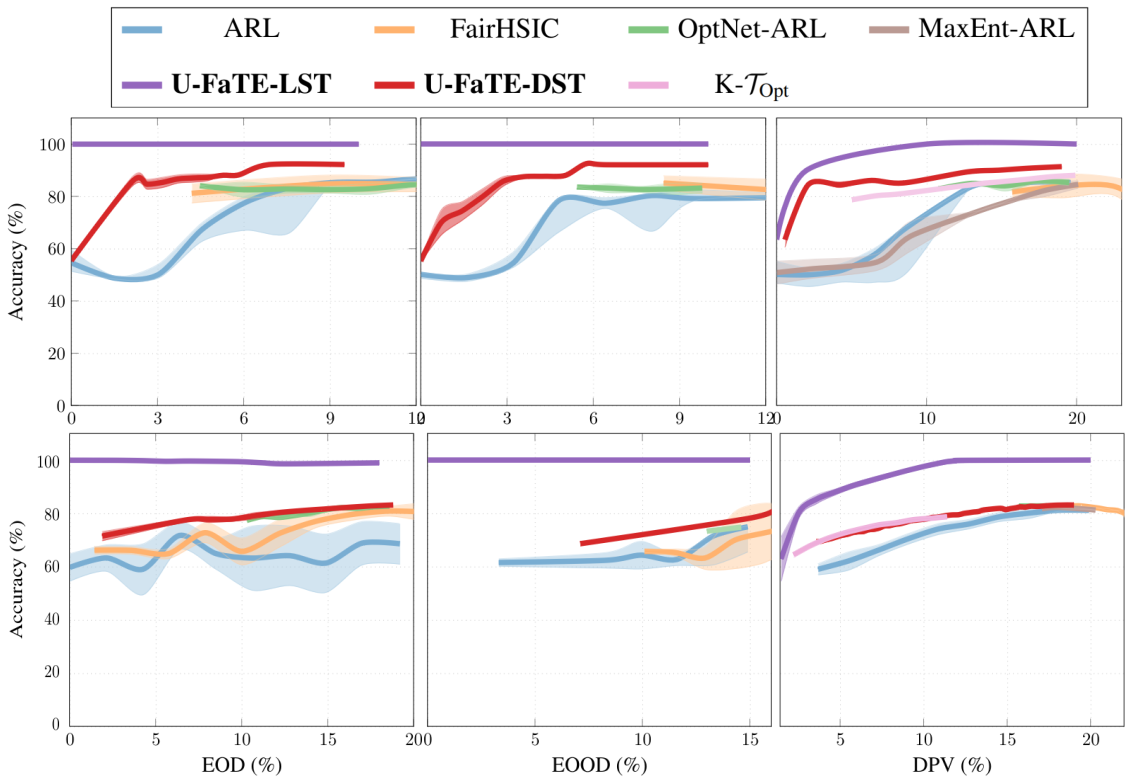 U-FaTE

Experimental Evaluation

How far are CLIP's zero-shot predictions from the trade-offs?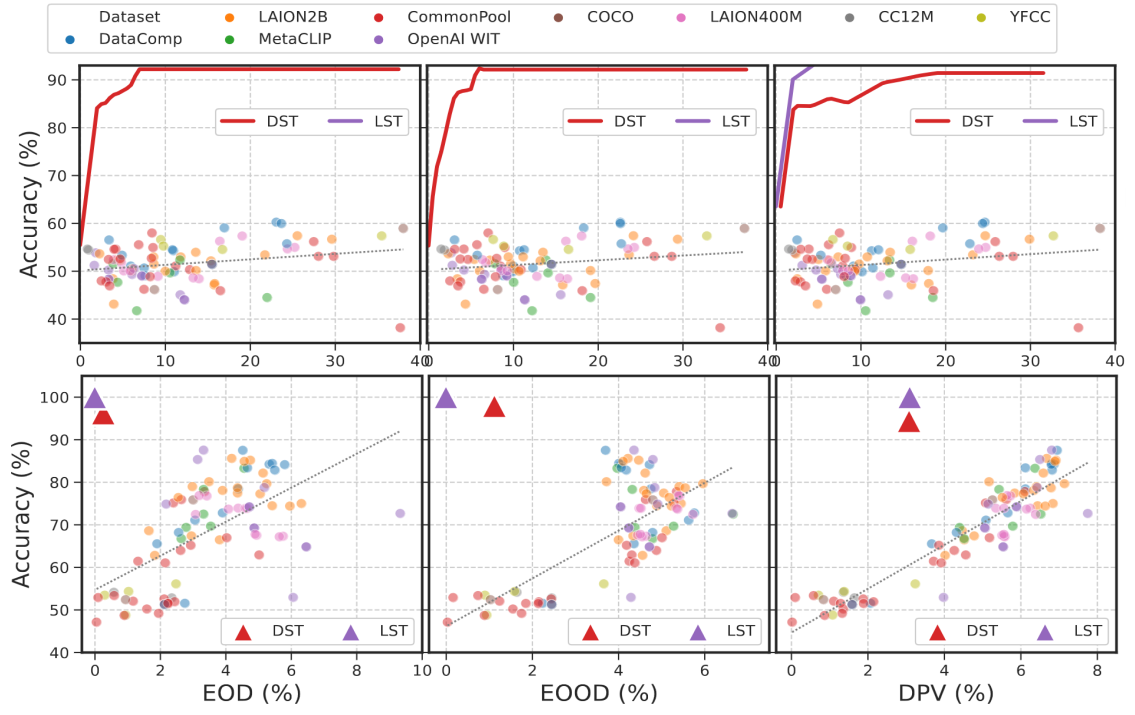 U-FaTE

Experimental Evaluation

How far are pre-trained supervised image models from the trade-offs? U-FaTE

Utility-Fairness Trade-Offs and How to Find Them

Michigan State University

How Fair is Your ML Model?

Questions that We Answer

Definitions

Fairness Definitions

How to Estimate these Trade-Offs?

Objective Function

Training

Experimental Evaluation

Experimental Evaluation

Experimental Evaluation

Thank you!